We welcome motivated students who would like to do research in computational physics. Interested students are encouraged to send inquiries via email or simply drop by the office and chat (see the Contact tab).

Our research interests are concentrated in the field computational quantum mechanics, which spans quantum chemistry, electronic structure, few-body physics, atomic and molecular physics, quantum dynamics, nanoscience, and solid state physics.

• One of our main and continuously sustained activity has been the development and applications of methods that utilize all-particle explicitly correlated Guassians in quantum mechanical calculations of various quantum systems. Explicitly correlated Gaussian (ECG) basis sets have a wide range of applications in chemistry and physics and provide a very powerful tool to solve quantum few-body problem with all kinds of interparticle interaction. 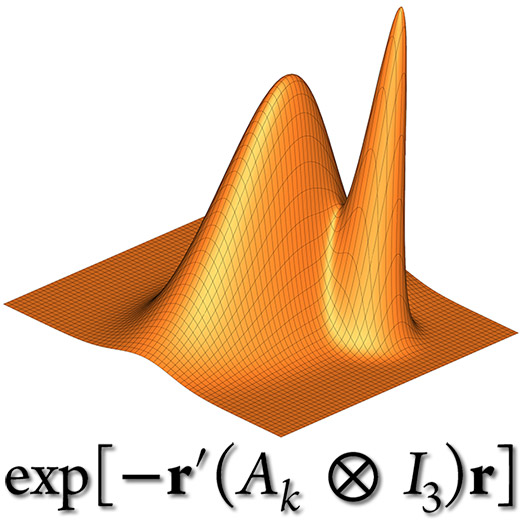In particular, we are interested in theoretical spectroscopy of few-electron atoms and molecules with and without assuming the Born-Oppenheimer approximation. High precision calculations on such systems require the use of state-of-the-art computational approaches. Treatment of relativistic corrections is also often necessary for comparison with highly accurate experimental data.
  Small systems containing positrons and other exotic particles are another class of quantum systems we have been investigating. Over the last decades there has been a lot of speculation about whether positrons could bind to atoms and if so what is the mechanism of this binding. The question of dynamical stability of positronic systems is non-trivial as positron binding is usually quite weak. Reliable calculations help to answer that question and provide accurate estimates of the average lifetimes and other properties.
  Recently, we also became interested in studying the properties of confined systems of electrons and holes in semiconductors. Within the effective mass approximation, ECG basis sets allow accurate determination of the binding energies and electron-hole recombination probabilities in quantum dots with multiple excitons and study the effect of the dot size and geometry.
  The scope of possible applications of ECGs is still not fully explored. Quantum few-body problem is of frequent occurence in many areas of physics. Thus, the ability to solve it accurately is of great importance. The ultimate goal of our effort is to develop a general, efficient, and predictive framework that can be succesfully used in various applications ranging from atomic systems to quarks.
• Light-matter interaction is at the heart of many conceptual, foundational and applicational endeavours in physics. With the emergence and ever increasing use of high power coherent light sources new prospects open up to steer and control the motion of electrons and nuclei in atoms, molecules, and condensed matter systems. However, it requires a good undestanding of the underlying quantum dynamics. 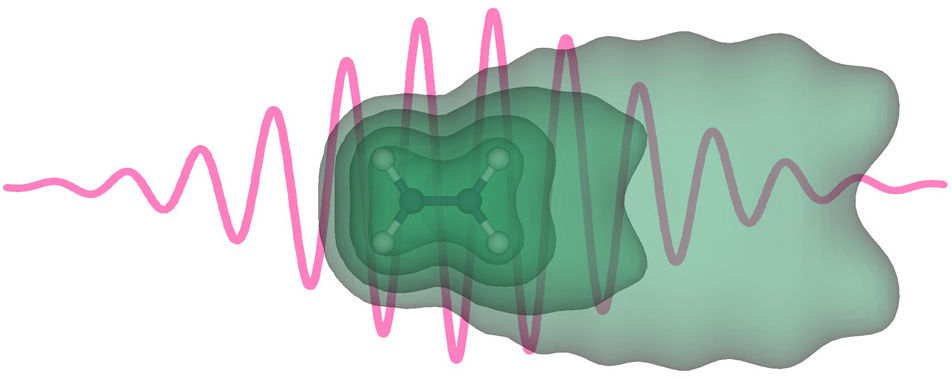This is why computer simulations of strong field phenomena have been playing an important role in femto- and atto-second science. In our work we pursue the theoretical and computational studies of various laser-induced phenomena in time domain. In particular, our work is centered around the applications of time-dependent density functional theory (TDDFT) to study the processes of excitation, ionization, fragmentation, and bond scission in molecules and nanosystems. Our simulations also deal with the modeling of Coulomb explosion in small molecules and other strong field processes. All of the above processes become significant at the laser field intensities comparable by order of magnitude to the field that binds electrons in atoms in molecules (around 10¹⁴-10¹⁶ W/cm²). Selective manipulation of chemical bonds can enable novel synthesis of molecular species and materials with new functionalities. At the same time, ultrashort (just a few femtoseconds) probes allow resolving the evolution of nuclear and electronic subsystems and provides an insight into the nature of light-matter interaction at the atomic scale.
• Nanoscience and nanotechnology, which aim to manipulate matter at the atomic scale, are revolutionizing science and industry. 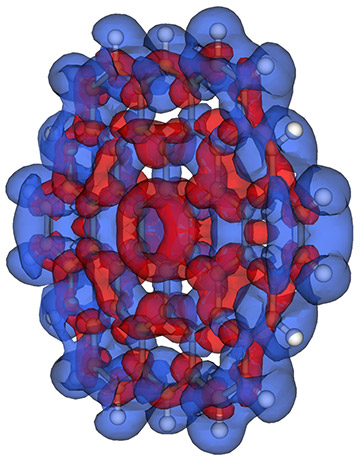Through the development of new devices used in everyday life these fields will have a huge societal impact in the near future. Currently, the majority of computational studies in nanoscience focus on the static behavior of materials. Such studies provide useful information about the structure and various properties. However, understanding of many phenomena in physics, chemistry, materials science, and energy-related fields often requires knowledge of the electron and ion dynamics. Part of our research effort is focused on applications and computer simulations of quantum dynamics in nanostructures. Thus research has included the modeling of field emission in carbon nanotubes, laser-assisted desorption of atoms from surfaces, simulating the interaction of energetic ions with materials (energy transfer, possibility of defect creation in 2D structures), and other applications. The main goal of this effort is to provide quantitative understanding and enhance our knowledge about the electron dynamics at the nanoscale
• Developing parallel computer codes for large scale scientific computations has been an integral part of our research. Computer modeling of complex systems not only requires the use of powerful computational resources but also sophisticated and highly efficient computational approaches. Adaptation of numerical algorithms and achieving adequate scalability for parallel execution in shared and distributed memory environment is a key ingredient (in fact, a necessity) that allows to perform simulations with permanently increasing system size and accuracy requirements.
  We maintain some (practical) interest in numerical linear algebra and optimization, as well as in many other areas related to scientific computing.
  Most of the simulations we perform make use of our in-house computer codes. We have developed and maintained the codes for few-body quantum-mechanical simulations with various forms of explicitly correlated Gaussians. We have also participated in the development of of the code for computer simulations in the framework of real-space real-time time-dependent density functional theory.